 URBS 502: Descriptive Statistics
URBS 502: Descriptive Statistics
“The government is very keen on amassing statistics. They will collect them, raise them to the nth power, take the cube root, and prepare wonderful diagrams. But you must never forget that every one of these figures comes in the first instance from the village watchman, who just puts down what he pleases.”
Sir Josiah Stamp
Commissioner of Inland Revenue
(1896-1919)
Scales of Measurement
Nominal data (naming data)
· Classifies data into mutually exclusive (non overlapping) exhausting categories in which no order or rank can be imposed on the data
· No logical ordering of categories
· Categories are qualitative in nature
· Examples: gender; religion; eye color; marital status
Ordinal (rank order data)
· Classify data into categories that can be ranked, however precise differences between ranks don’t exist
· Differences in amount of measured characteristic are discernible and numbers are assigned according to that amount
· Properties of ordinal data:
o Data are mutually exclusive
o Data categories have some logical order
o E.g. Results of a 400m race: 1st , 2nd, 3rd
Interval (Discrete) Data
· A quantitative variable whose set of possible values is countable
· Consist of data that are whole numbers and have no decimal places
· Often thought as counting data
o Number of people in a lecture theatre
o Number of lecture halls on MSU campus
o Number of people who agree with a particular statement
Interval (Continuous) Data
· A variable that can take any real number
o Height
o Weight
o Income
The Normal
Curve
Statistical tools are grouped according to function. Some tools serve to describe a large group of information in just a few numbers. These tools are called “descriptive statistics,” and they include the four “measures of central tendency” (mean, median, mode, and range). Other tools tools test to see whether the information obtained is close to what should be expected. These tools are called “inductive statistics.” They have that name because they are based on inductive logic: key terms in the formulas are derived from observation rather than deduced from a definition. In this unit, we will consider descriptive statistics (average and standard deviation).
“Distribution” is the statistician’s name for all of the observations you have made about a single characteristic (like the number of people per household, the age of the people in the region, or the number of people using a department’s services each day last month). If all the observations for any of these characteristics were ranked from highest to lowest, and then plotted on a graph, it might look like this:
Fig. 1: Normal Distribution
What you see is called “Galton’s Board” (after the English mathematician, Francis Galton). It is created by dropping bearings through the point in the top of the pyramid, where they bounce around on the pins below, until finally they fall into one of the 9 races. The bright line shows a “normal curve,” and as you can see a very large number of chance interactions approximates just such a distribution. When physical bodies (bearings, grains of sand, seeds of wheat, etc.) react independently on each other, they will distribute themselves so that the greatest number are in the middle of the distribution, and will drop off rapidly toward either end.
Descriptive statistics are designed to express the same information displayed in Figure 1, only to do it with a few mathematical expressions. Charts are useful because they can present a large amount of information (“data”; one item from the data is called a “datum”) in a fairly compact form that is often easy to grasp, at least in its broad outlines. On the other hand, the information from charts cannot be directly inserted into other mathematical statements, nor do charts lend themselves to a precise summary. That is what descriptive statistics are for.
The most common descriptive statistics are the three “measures of central tendency”: mean (or average), median, and mode. The mode is the measurement category that occurs most frequently (in Figure 1, it is right in the middle). The median is the observation that falls exactly in the middle of the distribution, when the observations are ranked from lowest to highest (in Figure 1, is also right in the middle). The means is the “weighted center” of the observations; if the number line were thought of as a balance, the mean would be the point where the line balanced (in Figure 1, it is again in the middle).
You have, no doubt, noticed that the three measures returned the same result in the example. This is not always the case; if it were, there would be no need for three different measures. The first example I gave you was a nicely balanced distribution. Such things are rare in the real world. Usually, the distribution is skewed to one side or the other, as in the following figures:
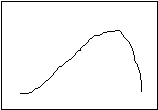
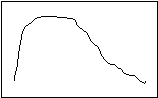
Positive Skew Negative Skew
In a positively skewed distribution, the median (the exact middle of the observations) is pulled to the right (the “positive” direction) of the mode (the most common distribution), and the median (the “balance point”) is pulled even more to the right. In a negatively skewed distribution, the arrangement is reversed—the mean and the median are pulled to the left (the “negative” direction). Notice, then, that the relative location of the three measures of central tendency can tell you if a distribution is skewed, and in which direction.
Since there are three measures, how do you decide which one to use? If the distribution is fairly balanced (each side is a reflection of the other), the three measures are roughly comparable. There are many other statistical tools, however, which use the mean (or other measures based on the mean) as part of the calculations. For that reason, the mean is the preferred measure of central tendency. However, if the distribution is badly skewed, the mean will not be a useful measure since it is affected most by imbalance. In those cases, the median is most commonly reported. Income, for example, is usually a skewed distribution; it is customary to report the median personal or household income rather than the average.
In addition to the measures of central tendency, descriptive statistics also include measures of dispersion. Two distributions can have the same mean, yet look very different, as in the following:
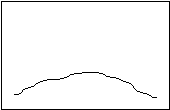
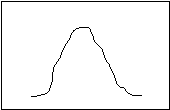
Platykurtosis Leptokurtosis
Although both distributions might have the same mean, the first one shows relatively similarly values all along the distribution, while in the second one the observations are lumped together near the mean. “Kurtosis” is a Greek word that means “curved.” “Platy” means flat, and “lepto” means “thin.” Standard deviation, the most common measure of dispersion, is a measure of the average (or “standard”) deviation of each datum from the mean. The larger the standard deviation, the more spread out the data. If two distributions have the same standard deviation, their general outline must be the same. There may still be some minor variation, but it will be slight. In this chapter, you will learn how to calculate the mean and the standard deviation.
Descriptive Statistics
Descriptive statistics are used to summarize the characteristics of a distribution of data. There are two descriptive statistics which will be explained here: mean and standard deviation.
The mean and standard deviation can be calculated only if the data are measured on an “interval” scale, or can be assumed to have been derived from an underlying interval scale. An interval scale is one in which the numbers represent an ordered relationship (2 is greater than 1, 5 is greater than 4, etc.), and the distance (or “interval”) between each number is the same (the interval between 2 and 1 is the same “length” as the interval between 5 and 4). Interval scales are so common that you are probably wondering what the fuss is all about: population, income, number of housing units are all measured on an interval scale. Attitude scales (“On a scale of 1 to 5, how do you rate….”), while not strictly interval scales, are often assumed to reflect an underlying interval relationship. But some common measures are not interval, and calculating an average can result in nonsense—like the mythical “0.4” child born to the average family, or finding that the average sex distribution is “1.329” (if “1” means “male,” should that “statistic” be interpreted as saying that the average male is oversexed?). If you cannot assume an underlying interval distribution, use the median or the mode to report the central tendency of the distribution. If you try to calculate a mean, you will get garbage; and if someone catches you at it, you will end up looking silly.
Mean (Average)
The mean is the total value of the observations, divided by the number of observations. The result is a weighted mid-point of the distribution of the data. The formula is:
x = Σx
n
“x” (read,
“X-bar”) is the standard symbol for the mean. “x”
is a standard symbol for a single observation; “å” (the capital
Greek letter, sigma) is a standard symbol for “the sum of.” “n”
is commonly used in statistics to represent the number of observations.
Standard Deviation
The standard deviation is the average deviation of the observations from the mean. It is calculated by:
1. Obtaining
the deviation of each observation from the mean ( x - x);
2. Squaring
each deviation (x - x)2 , which minimizes the impact of minor
deviations and emphasizes the larger ones (“squared deviations” are
called “variance”);
3. Calculating
the total variance å
( x - x)2
4. Calculating
the average variance å (x - x)2
n
5. Obtaining
the “standard,” or average, deviation by taking the square root of
the variance (You can think of this as scaling the variance back down to the
size of the sample, or as reversing the process of squaring the individual
deviations which was done earlier to emphasize larger differences over smaller
ones). The complete formula
reads:
6. σ
= √ Σ(x - x)2
/ n (s is
the lower-case Greek letter “sigma,” and is the symbol for standard
deviation)
Both the mean and the standard deviation are given here in the form that describes the distribution of data as it was obtained. When you are using empirical (or observed) values as estimates of the true parameters of an underlying distribution (as you will in the t-Test, correlation, and ANOVA), you have to adjust the formula. The adjustment is to replace the sample size (“n”) with “n-1” to account for the tendency of a sample to underestimate the true values of parameters.
Practice Exercise
You already know how to access the American Fact Finder and
other census data. Go to the census
website and select at least 2 variables with at least 50 observations on each
variable. The observations should
be from the same units (so you can compare the variables in later
assignments). And don’t limit
yourself to just the Census of Population and the Census of Housing. For example, you might go to the Census
of Governments and gather data on the “Price of Government” for 50
cities in
Then write a memo describing the data you collected. The memo should include:
1) Some description of what sort of relationship you expect
between the variables you selected (ie., why did you select these
variables? What do you hope to
demonstrate?)
2) Qualitative
presentation of your data:
a) Tabular (if any of your data are
grouped, why did you use those groupings?)
b) Graphic (why did you choose this or that
particular form of graphic presentation for these particular data?)
3)
Quantitative presentation of your data (why did you choose the
mean/median/mode? IQR/variance/standard distribution?)
4) Verbal description
of your data (don’t just give me the tables and the stats—what does
all that gobbledygook mean?)
© 1996 A.J.Filipovitch
Revised 25 January 2010
